Painting Demo

This weekend, I decided to take a break from all the oil paintings I've been working on to do a new painting and try out the proportions I've been writing about in previous blogs. Here's the subject matter (left) - eggshells. What else???

I began by creating a Root 2 Rectangle. First, I drew a 15" square, then measured the diagonal which was 21.25". I took the square root of the diagonal and added that number to the length of one side of the square. The resulting rectangle is 19.6" x 15." (below)

Next, I decided to create a simple armature for the Root 2 rectangle. (below)

I decided to use the long axis as the vertical on my painting, so I upended the armature and also decided which part of the armature I wanted to utilize for my design (in orange). I also identified the important nodes with red circles. (below)

Then, I drew eggshells on tracing paper laid overtop the armature paying special attention to placement on the nodes. (below)

Next, I created a value drawing using charcoal paying attention to the directionality I selected in the armature as well as the nodes. (below)

At this point, I was ready to transfer the drawing to my watercolor paper (Arches 300 lb. cold press) using graphite paper. (below)

Before painting, I had to determine the palette. I settled on Faience Blue, Viridian, Cadmium Yellow Light, Cadmium Orange, and Permanent Red. You may well ask if there is a special reason I used these hues. Actually ... not really. I'm running out of watercolor paint and I still had plenty of these left! But, I did want the primaries and two secondaries, and I didn't want to exceed five hues. Often, I'll limit my palette to three hues. The fewer hues used, the greater chance of creating harmony. (below)

As I began to apply paint, I paid special attention to the value drawing I made earlier. This is critical! First, I applied masking fluid to areas that I wanted to keep white. Then, I applied a light blue wash to areas that will recede (below left). After that, I just started painting in all the eggs. I've posted several steps below showing my progress.

The completed painting (below).

Next, I have to check my work. So I loaded a digital image of my painting onto the computer and changed it to grayscale. When I compare the grayscale image (below left) to the original value study (below right) they match. I don't need to work on the values again.

Finally ... what did I learn from this? Well, it's got me thinking more about design. Although I didn't attempt a complex armature for this painting, I did manage to adhere to my intended design. Being able to paint intentionally is a huge step toward painting masterfully. OK - so I didn't shake up the art world with this painting, but who knows what the future will bring :-)

A List

As you know by now, I love reading art books. And, I've found that many of you have quite a collection as well. Therefore, I'm listing below the art-related books I've read over the past six months and hope that you'll mention the books you find helpful as well!

Ways of Seeing by John Berger, 1972, Penguin Books

Art Theory: An Historical Introduction, 2nd ed. by Robert Williams, 2009, Blackwell Publ. Ltd.

The Shape of Content by Ben Shahn, 1957, Harvard University Press

Interaction of Color by Josef Albers, 2006, Yale University

Art and Visual Perception: A Psychology of the Creative Eye by Rudolf Arnheim, 1974, University of California Press, Ltd.

From Ordinary to Extraordinary: Art & Design Problem Solving by Ken Vieth, 1999, Davis Publications, Inc.

Classical Painting Atelier: A Contemporary Guide to Traditional Studio Practice by Juliette Aristides, 2008, Watson-Guptill Publications

Georgia O'Keeffe: Nature and Abstraction, 2007. a joint publication of the Irish Museum of Modern Art and the Vancouver Art Gallery

Louise Nevelson: A Passionate Life by Laurie Lisle, 1990, Summit Books

Expression

It would be easy to continue rambling on about Arnheim's ideas in his book Art and Visual Perception, but it's time to make a final comment and move on. Appropriately, his final chapter is entitled Expression. The previous five hundred pages dealt with the intricacies of visual perception concerning balance, shape, form, space, light, color, movement, and dynamics. In the final chapter, Arnheim writes: From the beginning it was evident that one could not do justice to what we see by describing it only with the measurements of size, shape, wavelength, or speed... As long as one talks about the mere measurements or practical earmarks of visual objects, it is possible to ignore their direct expression.

As an artist, it is my aim to express my viewpoint through paintings. I can't do that very well if I limit myself to draftsmanship or copying exactly what I see. My eggshell paintings are a good example of that. While it's true that we marvel at the skill it takes for an artist to precisely replicate in two dimensions what she sees in three, it's good to remember that more is required for a painting to be deemed a "work of art." That more is meaning, and meaning is revealed through expression. Most of us have a tendency to look at great works by the ancient masters as precise replications of reality. Often, this wasn't the case because expression was the desired effect. Let's look at a couple of examples:

Pieta by Michelangelo is arguably one of the most expressive sculptures in existence. It's almost impossible not to have an emotional reaction when viewing it. Because it looks so realistic, we might be tempted to think that all the proportions are accurate. Look again. There's no way that Mary is the correct proportion for holding an adult male (her son) of that size. Additionally, her face is that of a woman who is much too young to have a son of that age. Michelangelo needed to exaggerate her size, proportions, and youthful beauty in order to express a point. Here's another example:

This silverpoint drawing is attributed to Leondardo DaVinci. She looks very realistic. Again, we might be tempted to think that Leonardo realistically rendered the proportions and features of this young woman's face. In fact, Leonardo believed that most portrait artists naturally tend to make their subjects look like themselves in some way, and he may have, to some degree, altered the appearance of many of his subjects to his own proportions. Again, expression was more important to this master than precise replication.

This brings me to a practice that I perceive as a problem. Artists are becoming more and more reliant on reference photographs when they draw and paint. In an earlier post I mentioned that I attended a watercolor workshop ten years ago where another student was painting from a reference photo of a harbor scene. He took great pains to paint boats, pilings, moorings, landmasses, piers, buildings, seagulls exactly as they appeared in the photograph. His only motivation seemed to be that of precisely replicating the photograph. What's the point of that? Just frame the photo and be done with it. What did this student have to say about his own relationship with this harbor scene? What was his personal viewpoint? As I see it, expression means that you transform what you physically perceive to what you emotionally perceive. It's a translation from what I see to how I think about what I see.

To sum this up: I truly appreciate Arnheim's ideas. They help artists understand the effects of the various elements that go into making a work of art upon the perception of the viewer. I think that's important, because I'm always looking for ways to improve my ability to effectively express my ideas in two dimensions. But, even if I forget some of the principles in this book, I won't forget his summary: expression.

Light

It's time for me to leave Arnheim's discussion of shape even though he has a lot more to say about it. If you want to read his book, it's entitled Art and Visual Perception: A Psychology of the Creative Eye. I'll devote a few more blogs to this book and then find something else. I'm trying not to overlap too much with the material I present in my workshops!

Light ... a LOT has been written about this topic, so I won't even attempt an exhaustive synthesis. But, Arnheim mentions a few things that interest me. He discusses both rendering the effect of light in a painting and the symbolism of light.


1. Rendering light - typically, artists model the volume of an object by rendering the effects of light upon it. This involves depicting highlights, body value, body shadow, cast shadow, etc. Here's an example that I painted from (what else?) an eggshell:


2. Symbolism - the source of the light can impart special meaning to a painting. That is, light that is cast upon an object may mean something entirely different from light that is emitted from the object itself. Here are two examples from Rembrandt's work:
In this painting entitled Adoration of the Shepherds, the major source of light is coming from the Christ child in the manger: a symbol of "divine light."

However, in The Prophet Jeremiah Mourning Over the Destruction, Rembrandt uses a narrow beam of light from above to illuminate part of a dark scene. Symbolically, the light from above is falling upon the dark humble human habitat, symbolizing the inferior position of man.

There are so many other symbols attached to light, that I can't begin to list them all here. Believe it or not, I was very concerned about the source of light in my eggshell series. Sometimes the light falls upon the shells from an external source, but more often than not, the light is internal. This is because the series utilizes fractured eggshells as a metaphor for the effects of pressure upon life, the human psyche, and our investments. After it has been cracked, the shell cannot be restored to its initial pristine structural state and fragmentation is the result. As psychological portraits, each painting in this series relies upon the transformation of ordinary eggshell fragments into a single complete entity that possesses a unique personality or mood. This is achieved by imposing a highly chromatic design onto the arrangement, and creating directional focus that, in some instances, adds the time dimension. Luminosity is the desired effect in most of these paintings because it implies a life-force which is the essence of the new entity that has emerged from the fragments.

Now, let's take a look at the practical matter of rendering light in a painting. Arnheim asks: How does Rembrandt obtain his glowing luminosity? Here are some of the ways:

• Value contrast (chiaroscuro). Placing high value colors within a surrounding region of darks.
• Keeping shadows to a minimum on the lit object.
• Confining the strongest light within the confines of the object emitting the light
• Putting little detail in the areas of highest brightness.
• Surrounding the pure hues of the light with dull color.
  

Light may also be used to convey the idea of "nothingness." Arnheim points out how objects can vanish into lightness. This is a practice commonly used by landscape painters who deal with atmospheric effects upon light. My Fibonacci spiral below is based on the same idea of objects vanishing into space, which happens to be light:

Arnheim also mentions that The impressionists played down the difference between light and shadow and blurred the contours of objects. Impressionism at its most extreme is pointillism, in which each dot is a light source of its own. Take a look at Seurat's The Eiffel Tower:
BTW - this kind of illustrates our discussion yesterday about design vs. color. Without design, these colors wouldn't have made much sense. But, color is at least as dominant as design in this painting.

OK - I've probably said enough even though there's soooooo much more! But, I'll leave it to all of you to "illuminate" us with your great comments :)

A Four Hundred Year Old Argument

It's Sunday, so I'll take a one-day break from unpackaging Arnheim's ideas to ask your opinion.

Here's an ancient argument and I'd like your opinion:

Almost four hundred years ago (1600's) there lived a man named Charles LeBrun, who was once the Director of the Ecole Royale in Paris, which was established by the Academie Royale de Peinture et de Sculpture. So, you might say that his opinion mattered! He got into an intellectual argument with another guy named Roger de Piles, a literary man and amateur painter who had a big following. So, you might say that Piles' opinion mattered, too! What was the argument? LeBrun believed in the primacy of design and Piles argued for the primacy of color in painting. In other words, LeBrun placed greater emphasis on the depth of the narrative structure of a painting and Piles thought that creating optical sensation through color was more important.
Design vs. color.

It seems to me that this four hundred year old argument is still being waged! Opinion has swayed back and forth all this time in a tug of war. But, I'm no expert. So ... what do you think?? Which side do you take?

P.S. the photo was taken aboard a brigantine a couple of years ago, sailing from Tahiti to Bora Bora and back. I'm the crazy sailor on the left struggling to keep the helm. Looks like a losing battle, doesn't it?? Consider it the struggle between design and color. Guess which of the two I am :-)

Shape: the effects of separation, similarity, and color

Hi everyone! Ready for more shape analysis??
Here are two more insights from Arnheim's book:

1. Broken shapes are mended across spatial distance by similarity of color. I created the left and upper right studies to illustrate this principle. The whole shape (left) was separated into pieces spaced apart (right). Because they are the same color the mind wants to put the shapes back together again into a circle. This is a useful principle in painting, because broken shapes are far more interesting than whole shapes, and we can let the viewer's mind put them back together to suggest a single shape.

I think that Marcel Duschamp's painting Nude Descending Staircase #2 (left) is a good example of this principle. The figure is broken into a number of geometric shapes of similar color, and our mind wants to put them all back together to see a whole body on each step descending the stairs.

2. Difference in color is counteracted by similarity of shape. The study on the right shows the same four shapes, but they are different colors. These similar shapes unite the painting. If all the shapes were both different colors and different in shape, there would be no unity. So, as Arnheim point out, similar shapes (unity) counteract the effects of different colors (disunity).

A good example of this principle is the Three Sphinxes of Bikini by Salvador Dali. Here, the same "head" is painted three times. Although the scale of the heads changes as they recede into the distance, the shape is still the same. The difference is in the color and slight internal changes in the form as it gets smaller. The similar shape of the three heads unites the painting and the differences make it more interesting. If all three heads were identical in color to the largest one, the painting would be far less interesting - almost monotonous.

I'm not going to compare myself to the greatness of Dali or Duschamp, but I will use my humble painting to illustrate that I've used a number of different colors in this pianting and have counteracted that effect by using similar shapes to create unity.

Quote for the day: When I haven't any blue I use red. - Pablo Picasso

Regurgitation to Shape

As I write these posts about what I'm reading, I keep thinking: hey, didn't I learn that thirty-five years ago?? Why does it seem new to me now? Why do I have to keep reminding myself of these principles? Am I really that dense? For lack of a better term, it's called "regurgitation." I "ate" those principles decades ago, but they were only partially digested. It takes years of experience to test them in order to understand. So, from time to time I need to regurgitate a few "principles", chew on them a bit more, derive some nourishment, and swallow. Sorry about the crude imagery, but it fits. This is part of my life-long process of artistic growth.

In 1584 A.D., a Milanese painter named Giovanni Paolo Lomazzo published a book entitled "Treatise on Painting." In it, he divides painting into 7 elements: proportion, motion, color, light, perspective, composition, and form. Here's a challenge for you: since that time, 425 years ago, how many different books about these same seven elements do you think have been published??? I don't know the answer, but am certain the number is considerable. Is this unnecessary repetition (excessive regurgitaton) of the same old stuff? Maybe some of it is, but not all. "Art" is organic - it changes over time, culture, and geography. Artist authors need to find new ways to communicate ancient ideas in the context of contemporary art and culture, and to add a few new ideas. I'm guilty of owning and reading a TON of art books. It's not a compulsion, it's a thirst for understanding.

On occasion, I've been criticized by artist "friends" for reading too much. My defense is that I paint almost every single day, sometimes for as long as ten hours that day. I learn a lot from that experience. I also read a couple of hours a day, and I learn a lot from that. If I can learn from BOTH painting and reading, why not do both???

OK - I got that off my chest so I'll return to Arnheim's discussion of "shape." He mentions the impact of using similar and dissimilar shapes in a painting. If the artist's composition utilizes only similar shapes, then the individual shapes become somewhat invisible. Think of a school of fish, for instance. They all look alike so when they school together you really can't distinguish between them. But, as Arnheim states, if you place a different shape in your composition, it's distinguishable by it's difference. So, you put a tuna in with a school of cod, and you'll definitely see the tuna because it's a different shape.

I've included one of my own paintings to illustrate another way to break up the monotony of similar shapes. I altered the painting to grayscale so you could see that most of the shapes in this painting are alike. There's really not much to distinguish one shape from another. So, how did I overcome this problem? I used both color and value. The yellow/orange eggshell pattern can be easily distinguished from the blue/violet field. Usually, we opt to vary a few shapes in a composition to create variety, but, as you can see, color and value work just as well. So does texture.

More, next time.

Shape and simplification

OK ... no more math! I'll get back to more of Arnheim's ideas about shape and perception. Apparently, it's the natural tendency of humans to simplify complex shapes when they see them. As Arnheim puts it: "According to the basic law of visual perception, any stimulus pattern tends to be seen in such a way that the resulting structure is as simple as the given conditions permit." That's a fancy way of saying that our minds try to organize what we see in order to simplify it so we can recognize, or make sense, of it. I'll extend beyond Arheim's concept and apply this to painting. When I first look at a stack of eggshells I see chaos. I know they're eggshells, but the jumble of edges and randomness doesn't make much sense to me. At first glance I couldn't tell you how many eggshells are in the stack, how many are right-side up or upside down, or any other number of details that might reveal order or pattern. I realize that if I painted the eggshells just as I see them, I would cause the same type of confusion in the viewer of my painting. So, I look for a way to impose simple order on the eggshell shapes. This is where artistry comes in! We artists must find creative ways to alter what we see so it has meaning and makes sense. The painting I've attached to this blog is called "All Cracked Up VIII." Can you see why I called it that??

But, let's move beyond my work to that of a true genius: Jackson Pollock. At first glance, it's hard to make sense of his drip paintings. But, when I stand before one so that it fully engulfs my entire field of vision, there's a powerful rhythm - a symmetry that you can see and feel. It makes sense!

Or, we can look at a bunch of dots on a Seurat painting and see them as parts of larger shapes. Our brains fuse the dots together in order to simplify the painting so we can understand it. We're always looking for something recognizable and in order to do that, our minds must simplify.

Does this mean that we have to create simple paintings? Not at all. Complexity can be just as effective as simplicity. BUT, complexity must be managed so it can make sense at some level.

I guess this ties in with what I mentioned in my last post. The Renaissance artists wanted to continue the elaborate style of their predecessors, the medieval artists, but they needed to simplify. To do that, they had to impose order. So, I guess I've come full circle back to mathematics! Once a nerd, always a nerd :)

Orderliness

Before I discuss today's topic, I should explain this painting. It's watercolor and was painted many years ago. The title is Measured Life at 51 and it's about a time in my life when I underwent chemotherapy for the first time. I began to think of all the ways my life was being measured: dosage of pills, timing of dosages, losing weight, measuring everything I ate, etc. Glad those days are behind me! It's not a very masterful painting, but it expresses how I felt at the time.

In the last post, I left you with Arnheim's idea that The great works of art are complex, but we also praise them for having simplicity, by which we mean that they organize a wealth of meaning and form in an overall structure that clearly defines the place and function of every detail in the whole. This way of organizing a needed structure in the simplest possible way may be called its orderliness.

Over the past year I made it a point to study composition, and specifically Renaissance designs. Talk about making the complex simple! Although I haven't yet applied too much of what I learned, I plan to start a whole new series of paintings in 2010 that employs the mathematical division of space developed by the Ancients. The idea that a work of art will be more beautiful if it is made according to numerical relationships began in mid-fifth century BCE. Renaissance artists utilized that math, as do a growing number of contemporary artists. Everything old is new again!

For those of you who are brave enough to follow this line of reasoning, I'll briefly depart from Arnheim's book to discuss how the Masters placed shapes to create "orderliness." It's not a comprehensive analysis; just some tidbits.

I'll start with a very simple concept. You want to paint on a rectangular canvas or paper. According to Renaissance artists, the length and width of that rectangle should be a specific proportion to yield the best results. These are called root rectangles. Here's how it works:

1. Start with a square of any dimension (example - each side is 3")

2. Measure its diagonal (for a 3" square, that would be 4.25")

3. Calculate the square root of the diagonal (the square root of 4.25" is 2.06")

4. Add that number to the length of the base of the square (3" + 2.06" = 5.06")

5. Draw a line that defines the length of the base of the new rectangle

6. Draw the other three sides of the rectangle. (your rectangle has a height of 3" and length of 5.06")

This is a root 2 rectangle.

You can keep going, like the figure below, by drawing the diagonal of the new rectangle, taking its square root, and drawing the next larger rectangle. That would be a root 3 rectangle, etc.

Figure from Hambidge, 1920

GUESS WHAT??
If you use pre-made canvases/papers they're already sized according to these proportions!

OK, so you've decided on the size of your rectangular canvas/paper. Now, you must create a balanced (harmonic) composition to create "orderliness." For now, I'll forego a discussion of the size and color of the shapes. How did the "ancients" figure this out? Pythagoras, a Greek mathematician/philospher who lived around 500 BCE, discovered harmony through proportions, or ratios. This is the foundation of our modern musical harmonic scale, and also the foundation for Roman architecture and Renaissance art.

Eventually, Pythagorean theory on harmonics made its way to the Renaissance, when artists wanted to create a less complicated way to organize the elaborate designs of their predecessors, the medieval artists. These designs, or ways of creating orderliness, were eventually identified as the armature of the rectangle by Charles Bouleau in his book The Painter's Secret Geometry. Here's a complex armature:

Notice that the diagonal lines are drawn from either the corners or middle of each side. The verticals are calculated by halves, thirds, fifths, (sevenths?). Nodes occur where lines cross, and it's on those some of these nodes that the artists would place focal points.
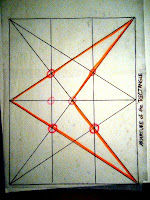
Here's the armature used by Johannes Vermeer in his painting, The Astronomer. Notice that he ony used a few of the diagonals, verticals, and horizontals from the more complex armature in the diagram above. Also, notice the central nodes that define the placement of the globe, wrist, and shoulder in the middle of the composition. The left hand is immediately below the right wrist on another node, and the toe of the left shoe is below that. The angle of the light follows the two diagonals drawn from the upper left to the bottom right. And so on. (Figure taken from Classical Painting Atelier by Juliette Aristides, 2008).

There are many variations on this basic armature, and certainly any artist can invent one. They may be very simple, or include all the lines found in the figure above. Some artists included circles and arcs in the armatures. What do they all have in common? Harmonic symmetry.

Does an artist have to use these geometric principles? No, not at all. As I said earlier, I plan to experiment with it in 2010 to see if I can correct many of the design flaws I've been noticing in my work. This gives me a great opportunity to marry my two "selves": the nerd and the aesthete!

So, for those of you who made it this far - thank you! and here's a great quote as a reward meant to provide a counterweight to all that precedes it:

There are some things in painting which cannot be explained, and that something is essential. - Pierre August Renoir

Shape, continued...

Before I return to Arnheim's discussion about shape, I'd like to pay special attention to Don Michael's (http://www.donmichaeljr.com/blog/) perceptive response to yesterday's post. He wrote:

"I noticed that you have used this same composition in two of your paintings, All Cracked Up XXIII (right above) and XXV (left above). In XXIII, the example you provided, the first time I saw it I noticed that you were driving my eye to those two pieces through value, placement, shape and color. The flatness of the larger piece, the intensity of the shadows, the brightness of the larger piece in context to its surroundings all drew my eye to it. In fact, it stopped my eye right there. In XXV you have taken the same composition with a very similar pair of shapes in the exact same position and yet my eye is not as readily drawn to them. The shadow is less pronounced, the value is very similar to its immediate surroundings and the shadow pattern of the whole piece keeps my eye moving past those two shapes. Very interesting how lighting, value, chroma and shadow pattern can so differently affect these two variations of basically the same composition."

Don is absolutely right!! I was experimenting with the same composition and this supports Arnheim's point about perceptual shape. BTW - for some reason this program turned the fragment images sideways, and I don't know how to fix it!!

Quite honestly, most of Chapter 2 in Arnehim's book is interesting, but not of practical use to me. However, his discussion of The Principle of Parsimony when using shape caught my attention. This principle states that the simplest structure (shape) and the simplest organization of that structure will best serve the artist's purpose. He goes on to say that "The principle of parsimony is valid aesthetically in that the artist must not go beyond what is needed for his purpose." And, "The great works of art are complex, but we also praise them for having simplicity, by which we mean that they organize a wealth of meaning and form in an overall structure that clearly defines the place and function of every detail in the whole. This way of organizing a needed structure in the simplest possible way may be called its orderliness."

Simplicity of the complex created by order: In the next blog, I hope to write more about this. I spent the past year studying just that. Thanks for reading. I'd love to hear your viewpoints!!

Shape

It's Monday morning, and I'll return to Rudolf Arnheim's book, Art and Visual Perception: A Psychology of the Creative Eye. Before I do, however, I must place this in perspective. The reason I've dedicated this blog to a more scholarly analysis of art is because I need to improve my ability to plan, execute, and critique my own work. By explaining what I learn to you, and receiving your ideas in return, I gain greater understanding. However, this academic approach must be balanced by the artist's intuition in order for the work to become meaningful and unique. There must be an infusion of the heart and soul of the artist in the painting as well. In a much earlier blog I mentioned that Ben Shahn encourages the artist to draw from the totality of experiences, culture, and nature of who he/she is when creating a work of art. That being said, I'll venture back over to the academic side.

Chapter 1 was all about balance. In it, Arnheim identified the perceptual forces, why an artist should strive for balance in a painting, the effects of weight and direction, and many other things that I discussed in earlier blogs. Chapter 2 is all about shape. I'll share only a couple of thoughts about this chapter (you'll be pleased to know that I won't include his lengthy discussion on physiology and psychology!).

What is shape? According to Arnehim, the physical shape of an object is determined by its boundaries. That's a fine definition if you're just looking at an isolated object. But, he adds, there's also perceptual shape, where one perceives an object within the context of a given space, or in relation to other objects, or in a specific orientation. When the shape isn't isolated, we perceive it differently as it relates to its surroundings. As artists, we consider perceptual shape all the time as we compose. We arrange objects or forms to create an effect that we want the viewer to perceive. We are illusionists. For instance, I realize that I can paint an eggshell by itself, but if I break it and place those fragments within a large number of other fragments, the individual fragment is lost and becomes part of a larger whole. The perceived shape of that individual fragment is completely changed. The two images I attached to this blog illustrate that. The fragments on the right appear in the larger painting on the left. Our perception of the shape of those fragments is altered when they're placed in a larger arrangement of fragments.

This seems like a simple point to make, but it can become very complex. I'll write about that next time :)

The Orchestration of Solutions

Last Tuesday, November 10th, I posted some ideas about balance in terms of weight and direction from Rudolf Arnehim's book. Margaret Ryall (http://margaretryall.blogspot.com/) responded with a wonderful critical analysis. I think her comments deserve special attention, so I'll highlight some of them here:

Margaret wrote: Overall I agree with most of these points when I read them in isolation, but I think they may only work in isolation. When you start considering them together it gets muddled. You can solve all kinds of bad choices in composition by adjusting other things. For example: I agree that size affects composition and larger is heavier and bright colours are visually heavier than dark ones, but if you have a small bright colour and a large darker one you can makt it work. I also feel that when location of the above two is a factor, it changes again.

I'll skip over a bit here and get to her conclusion: I will conclude that no matter what you do in a composition you can do something else to fix the problem. It is more like an orchestra than discrete instruments. You almost need to have a number of paintings to look at to consider each of these points. I bet you will find examples against them that still work in composition.

Folks, I couldn't agree more with Margaret's remarks and am grateful that she took the time to offer this considered response. The idea of an orchestration appeals to me. The artist is the conductor and the subject, elements and principles are the orchestral members. It is up to the conductor to make it into music. This means some instruments may not be used at all. Others may dominate while others merely support, and so on. I think that Arnheim really intended this but I failed to explain his points within that context. The book is entitled Art and Visual Perception: A Psychology of the Creative Eye. He takes over 500 pages to explain the effects of minutia in drawing/painting and, as an artist, I'm interested in those effects. However, I realize that I can't engage in paying attention to every single psychological effect that I might create either accidentally or intentionally. That would inhibit creative expression. At the same time, being aware of these effects may help in problem solving as I compose and paint. It helps me to identify why something isn't working at all.

Dan Kent correctly pointed out yesterday that all my wine glasses seem to be tipping in these paintings. True! In fact, all the elements are placed on an arc, creating a "barrel" effect. In retrospect, I should either have exaggerated that effect a little more or eliminated it. It's too ambiguous and fence-sitting isn't good. Lesson learned :)

Thanks to ALL of you for contributing to this discussion!

Why should artists strive for balance?

This is an important question that Arnheim poses in the first chapter of his book Art and Visual Perception: A Psychology of the Creative Eye. I'll paraphrase his answer. One reason is that by stabilizing the relations between the various aspects of a painting, the artist creates a work of art that is unambiguous. Ambiguity confuses the artistic statement because it leaves the observer hovering between two or more assertions that do not add up to a whole. But, Arnheim provides an additional answer, which involves our psychological make-up. He states that man strives for equilibrium in all phases of his physical and mental existence, and that this same tendency can be observed not only in all organic life, but also in physical systems. From there he ventures into a wonderful discussion on the principle of entropy and the universe. However, this is not the final point. On page 410 of his book, Arnheim introduces "dynamics," the counter-principle to balance. Although I haven't yet fully digested that principle, I can tell you that there must exist a tension between the elements on the painting that the artist must balance. I prefer to see it as a dynamic equilibrium. Take a look at my wine painting at the upper left. There's a lot of tension and interplay between the shapes, hues, etc. That's tension. I had to balance those tensions by considering the weight of each element (discussed on the blog two days ago). I think it's balanced pretty well, but I suppose I could do better. It's all about experimenting and having fun with it. Like a "mad scientist" in her lab at midnight howling at the moon! Now, there's and idea for a painting :)

Balance: Left vs. Right

These are paintings from my Wine Series (gouache on Arches paper, 19" x 15") and I'm using them to illustrate another point from Arnheim's book. My previous post was a synthesis of Arnheim's ideas about visual weight and description when establishing balance in a drawing or painting. Continuing with the balance theme, he examines the influence of the left cerebral cortex of the brain which is dominant in most people upon our perception of elements placed in the left and right halves of the visual field of a work of art. BTW - the left cerebral cortex controls speech, writing, and reading. Here's a paraphrase of three points:

If there are two objects equal in size and one is shown in the left half and the other in the right half of the painting, the one on the right will look larger. In order to make them appear equal, the one on the left has to be increased in size.

Most people read pictures from left to right. Therefore, it's easier for us to see, for example, a rider traverse a picture from left to right. If the rider traverses from right to left, the viewer must overcome resistance and invest more effort to read the painting. It slows down the viewer.

The right side of a picture is more conspicuous and carries greater visual weight. To compensate, the artist must pay more attention to the left.

If I had to "nutshell" Arnheim's book, it's really about how the artist must create optical illusions to get his/her point across. This author tells us how the "normal" brain works and what the artist must do to compensate for that. I'll share a little more on the next post.